Code
# Paquetes sugeridos para la clase
# install.packages(c("tidyverse","patchwork","gt","pROC","broom","modelsummary"))
library(tidyverse)
library(patchwork)
library(gt)
library(broom)Contexto de la modelación basada en los datos
Orlando Joaqui-Barandica
August 24, 2025
Propósito. Este documento es la Clase Introductoria: una sesión para alinear expectativas, pensar en problemas reales y mapearlos a técnicas. No es un set de diapositivas; es un material reproducible: texto + código + figuras.
Objetivo: iniciar con preguntas casuales pero profundas. Por cada contexto, ¿qué mirarías antes de elegir la técnica?
Una cadena minorista ha notado variaciones importantes en las ventas de uno de sus productos y sospecha que el precio, las promociones y la estacionalidad están influyendo. Para tomar decisiones informadas, necesita analizar datos de 24 meses que incluyen ventas, precio promedio y gasto en promoción, con el fin de identificar patrones y estimar cómo cambios en el precio podrían impactar la demanda.
Entonces:
Imagina que trabajas para una cadena de tiendas y te piden encontrar el “punto justo” de precio para uno de sus productos estrella. Tienes sobre la mesa dos años de datos: cuánto se vendió cada mes, el precio promedio, el gasto en promociones y si fue temporada alta o baja. La gerencia quiere entender cómo ajustar el precio para vender más sin perder rentabilidad, y tu misión es descubrirlo usando los datos.
Pregunta: ¿Cuál es el problema?, ¿Cuál es la estructura de datos a la cuál te estás enfrentando?, etc. etc. etc.
# Simulación mínima para ambientar
df_vtas <- tibble(
mes = 1:24,
promo = rbinom(24, 1, .4),
precio = round(rnorm(24, mean = 10, sd = 1.2), 2),
estac = rep(c("alta","baja"), each = 12)
) |>
mutate(ventas = round( 2000 * precio^(-1.3) * ifelse(promo==1, 1.15, 1) * ifelse(estac=="alta", 1.2, 0.9)
* exp(rnorm(24, 0, .1)) ))
g1 <- ggplot(df_vtas, aes(precio, ventas, shape = estac, color = factor(promo))) +
geom_point(size = 3, alpha = .8) +
scale_color_manual(
values = c("0" = "gray50", "1" = "tomato"),
labels = c("Sin promoción", "Con promoción"),
name = "Promoción"
) +
labs(
title = "Relación Precio–Ventas (simulación)",
x = "Precio",
y = "Ventas"
) +
theme_minimal()
g1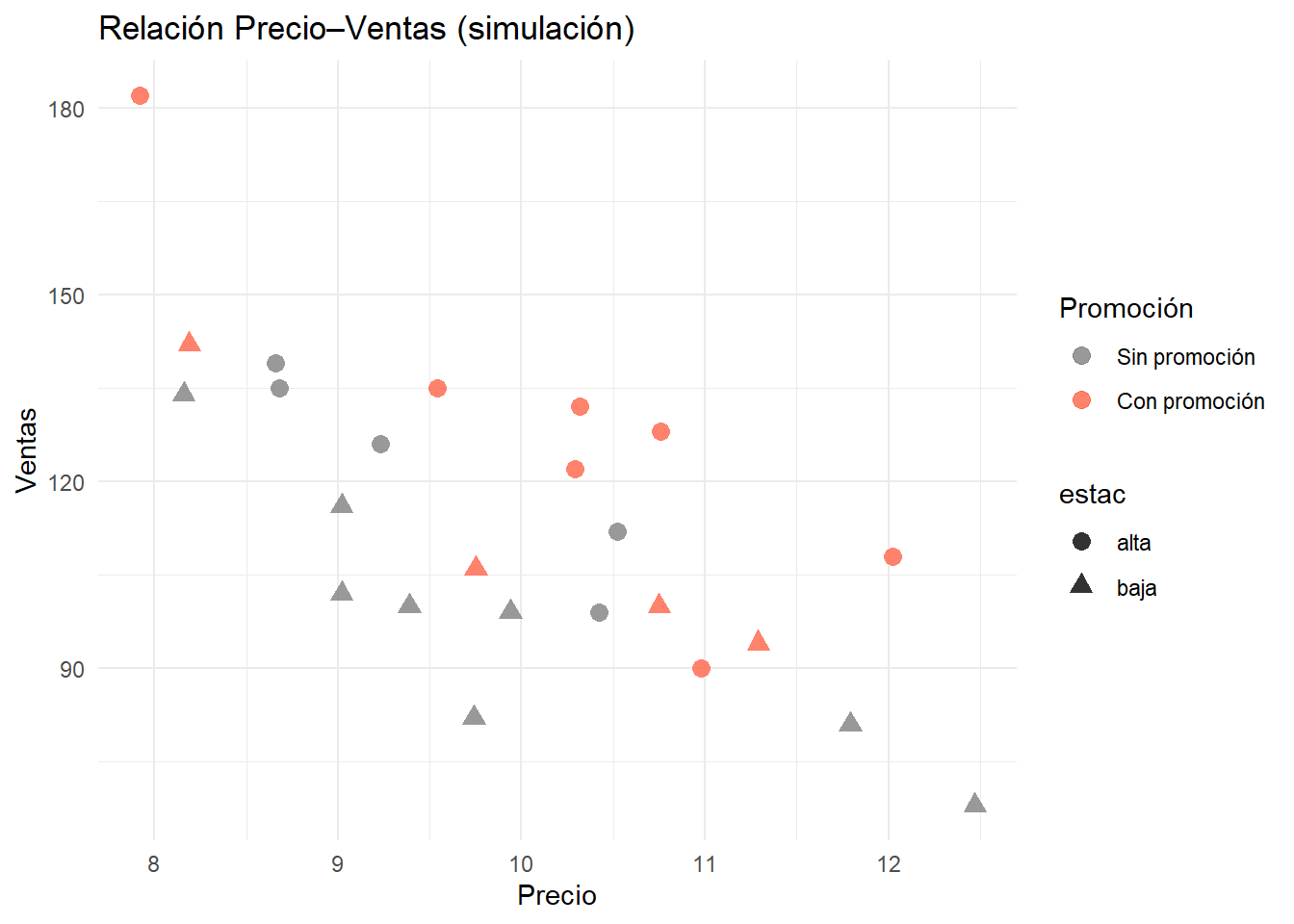
En un plan de incentivos, la gerencia quiere saber si el bono ayuda más a quienes menos ganan o si el efecto es similar para todos. La pregunta ya no es “¿cuánto sube el salario promedio?”, sino “¿qué pasa en los extremos?”: ¿mejora especialmente la situación de los de abajo?, ¿casi no cambia en los de arriba?, ¿se mueve toda la distribución por igual?
Pregunta: Si lo que importa es cómo cambian las colas (los salarios más bajos y más altos), ¿tiene sentido seguir mirando solo el promedio? ¿Qué métricas o gráficos usarías para comparar abajo, centro y arriba de la distribución?
# Ambientación: relación simulada con heterocedasticidad
# Simulación: el bono favorece más a quienes menos ganan
set.seed(123)
library(dplyr)
library(tidyr)
library(ggplot2)
n <- 1000
base <- rlnorm(n, meanlog = 11, sdlog = 0.45) # salarios base (sesgados a la derecha)
# El bono impacta más fuerte en la parte baja, medio en el centro y leve en la alta
q30 <- quantile(base, 0.30)
q70 <- quantile(base, 0.70)
efecto <- ifelse(base <= q30, 0.12,
ifelse(base <= q70, 0.05, 0.01))
despues <- base * (1 + efecto)
datos <- tibble(
salario = c(base, despues),
estado = rep(c("Antes del bono", "Después del bono"), each = n)
)
# Cálculo de cuantiles para marcar (10%, 50%, 90%) en cada estado
df_q <- datos %>%
group_by(estado) %>%
summarize(
q10 = quantile(salario, 0.10),
q50 = quantile(salario, 0.50),
q90 = quantile(salario, 0.90),
.groups = "drop"
) %>%
pivot_longer(cols = starts_with("q"), names_to = "quantil", values_to = "valor")
# Histograma superpuesto con líneas en 10-50-90
g2<- ggplot(datos, aes(salario, fill = estado)) +
geom_histogram(position = "identity", alpha = 0.35, bins = 40) +
geom_vline(data = df_q, aes(xintercept = valor, color = estado, linetype = quantil),
linewidth = 0.6, show.legend = TRUE) +
scale_fill_manual(values = c("Antes del bono" = "gray50", "Después del bono" = "steelblue")) +
scale_color_manual(values = c("Antes del bono" = "gray50", "Después del bono" = "steelblue")) +
labs(
title = "Distribución salarial antes y después del bono",
subtitle = "Líneas verticales: 10º, 50º (mediana) y 90º percentil por estado",
x = "Salario", y = "Frecuencia", fill = "Estado", color = "Estado", linetype = "Cuantil"
) +
theme_minimal()
g2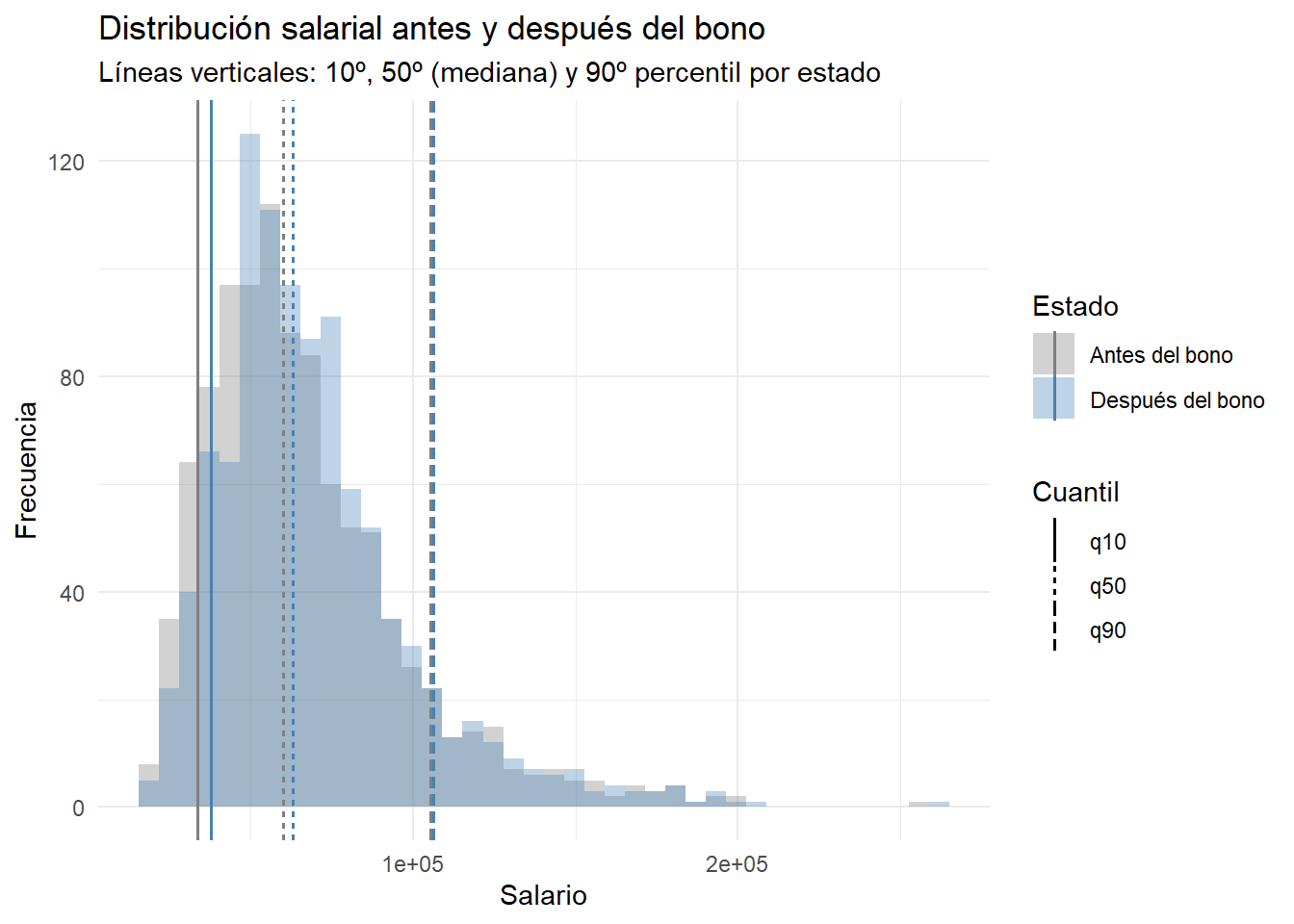
¿El bono “empuja” más la parte baja que la alta?
Si solo miraras el promedio, ¿te perderías este matiz?
¿Qué otras comparaciones harías entre abajo–centro–arriba para decidir si la política cumple su objetivo?
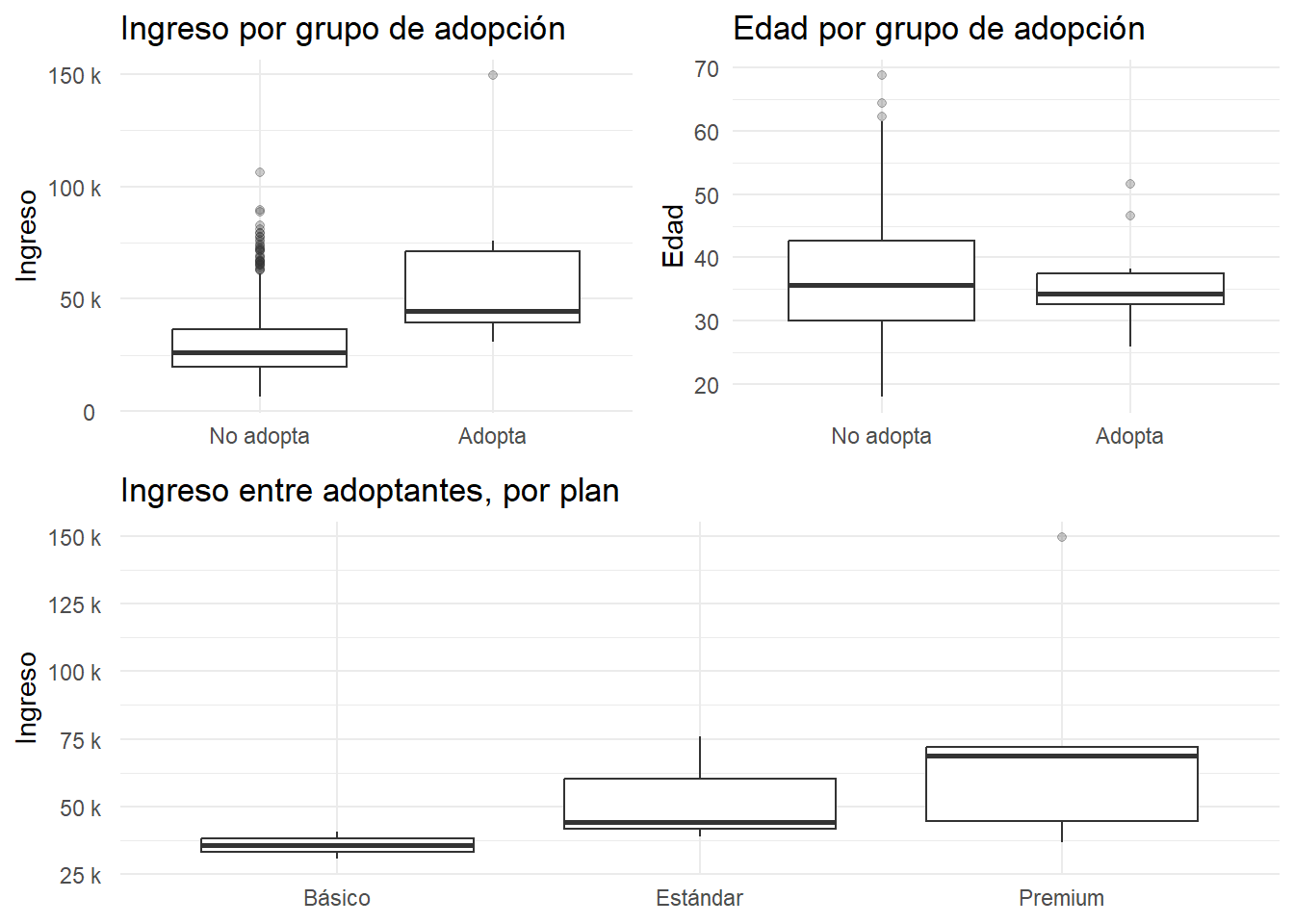
Un banco lanza un nuevo producto digital y ve baja adopción. No puede ofrecerlo indiscriminadamente: cada contacto cuesta, y hay tres planes (básico/estándar/premium) con estructuras de comisión distintas. El equipo quiere entender quiénes tienden a adoptar (sí/no) y, entre quienes adoptan, qué plan eligen. Sospechan que ingreso y edad influyen, pero también hay estacionalidad de campañas y límites de presupuesto. Antes de hablar de métricas avanzadas, la primera pregunta práctica es: ¿las distribuciones de ingreso/edad se ven distintas entre quienes adoptan y quienes no? Y, entre los que sí, ¿se diferencian según el plan?
Pregunta: Si las distribuciones por grupo son claramente distintas, ¿no sugiere eso probabilidades de adopción diferentes? ¿Cómo lo mostrarías de forma simple y convincente antes de construir el modelo?
# Simulación y boxplots (adopción y elección de plan) — versión robusta
set.seed(1)
library(tidyverse)
library(gridExtra)
n <- 1200
pros <- tibble(
ingreso = rlnorm(n, meanlog = 10.2, sdlog = 0.45),
edad = pmax(18, rnorm(n, mean = 36, sd = 9))
) |>
# prob. de adopción: crece con ingreso y edad
mutate(lp = -8 + 0.00006*ingreso + 0.028*edad,
p_adopta = 1/(1 + exp(-lp)),
adopta = rbinom(n, 1, p_adopta)) |>
# utilidades para planes SOLO si adopta (balanceadas + ruido)
rowwise() |>
mutate(
u_basico = 0.10 + 0.000015*ingreso + 0.004*edad + rnorm(1, 0, 0.15),
u_estandar = 0.00 + 0.000020*ingreso + 0.003*edad + rnorm(1, 0, 0.15),
u_premium = -0.10 + 0.000035*ingreso + 0.001*edad + rnorm(1, 0, 0.15),
plan = if (adopta == 1) {
exps <- exp(c(u_basico, u_estandar, u_premium))
c("Básico","Estándar","Premium")[sample(1:3, 1, prob = exps/sum(exps))]
} else NA_character_
) |>
ungroup() |>
mutate(
grupo = factor(adopta, levels = c(0,1), labels = c("No adopta","Adopta")),
plan = factor(plan, levels = c("Básico","Estándar","Premium"))
)
# Boxplots: ¿ingreso/edad difieren entre No adopta vs Adopta?
p_ing <- ggplot(pros, aes(grupo, ingreso)) +
geom_boxplot(outlier.alpha = 0.25) +
scale_y_continuous(labels = scales::label_number(scale_cut = scales::cut_si(" "))) +
labs(title = "Ingreso por grupo de adopción", x = NULL, y = "Ingreso") +
theme_minimal()
p_edad <- ggplot(pros, aes(grupo, edad)) +
geom_boxplot(outlier.alpha = 0.25) +
labs(title = "Edad por grupo de adopción", x = NULL, y = "Edad") +
theme_minimal()
# Entre los que adoptan: ingreso por plan (forzamos el orden de niveles)
p_plan <- pros |>
filter(adopta == 1) |>
ggplot(aes(plan, ingreso)) +
geom_boxplot(outlier.alpha = 0.25) +
scale_x_discrete(drop = FALSE) + # respeta los 3 niveles
scale_y_continuous(labels = scales::label_number(scale_cut = scales::cut_si(" "))) +
labs(title = "Ingreso entre adoptantes, por plan", x = NULL, y = "Ingreso") +
theme_minimal()
gridExtra::grid.arrange(
p_ing, p_edad, p_plan,
layout_matrix = rbind(c(1,2),
c(3,3))
)
Aplicaste una encuesta con 30 preguntas tipo Likert (1–5) sobre hábitos de compra, sensibilidad al precio, uso de canales digitales y percepción de calidad/servicio. El equipo quiere crear segmentos útiles para marketing y diseño de producto (por ejemplo, “ahorradores”, “buscan conveniencia”, “premium”), pero con tantas preguntas hay redundancia y ruido: varias ítems parecen medir lo mismo y es difícil explicar los resultados a gerencia.
Pregunta: ¿Tiene sentido comprimir las 30 preguntas en pocas dimensiones interpretables (p.ej., “sensibilidad al precio”, “afinidad digital”, “búsqueda de calidad”) y luego segmentar? ¿Cómo decidir cuántas dimensiones y cuántos segmentos mantener sin perder interpretabilidad?
# Simulación realista: 30 ítems Likert con 3 factores latentes
set.seed(7)
library(tidyverse)
n <- 800
# tres perfiles latentes (solo para simular): Ahorrador / Conveniencia / Premium
perfil <- sample(c("Ahorrador","Conveniencia","Premium"), n, replace = TRUE, prob = c(.4,.35,.25))
# factores latentes por persona (no observables)
f_precio <- rnorm(n, ifelse(perfil=="Ahorrador", 0.8, ifelse(perfil=="Conveniencia", 0.1, -0.4)), 0.6)
f_digital <- rnorm(n, ifelse(perfil=="Conveniencia",0.7, ifelse(perfil=="Premium", 0.3, -0.2)), 0.6)
f_calidad <- rnorm(n, ifelse(perfil=="Premium", 0.8, ifelse(perfil=="Conveniencia", 0.2, 0.1)), 0.6)
# 30 items (10 por factor) + ruido; mapeo a escala 1-5
mk_items <- function(base, s = .6) pmin(5, pmax(1, round(scales::rescale(base + rnorm(n,0,s), to = c(1,5)))))
encuesta <- tibble(
perfil,
# 10 ítems que cargan en "precio"
precio_01 = mk_items( 1.2*f_precio),
precio_02 = mk_items( 1.0*f_precio),
precio_03 = mk_items( 0.9*f_precio),
precio_04 = mk_items( 1.1*f_precio),
precio_05 = mk_items( 0.8*f_precio),
precio_06 = mk_items( 1.0*f_precio),
precio_07 = mk_items( 1.0*f_precio),
precio_08 = mk_items( 0.9*f_precio),
precio_09 = mk_items( 1.1*f_precio),
precio_10 = mk_items( 0.7*f_precio),
# 10 ítems que cargan en "digital"
digital_01 = mk_items( 1.1*f_digital),
digital_02 = mk_items( 1.0*f_digital),
digital_03 = mk_items( 0.9*f_digital),
digital_04 = mk_items( 1.0*f_digital),
digital_05 = mk_items( 1.1*f_digital),
digital_06 = mk_items( 0.8*f_digital),
digital_07 = mk_items( 1.0*f_digital),
digital_08 = mk_items( 1.2*f_digital),
digital_09 = mk_items( 0.9*f_digital),
digital_10 = mk_items( 1.0*f_digital),
# 10 ítems que cargan en "calidad"
calidad_01 = mk_items( 1.1*f_calidad),
calidad_02 = mk_items( 1.0*f_calidad),
calidad_03 = mk_items( 0.9*f_calidad),
calidad_04 = mk_items( 1.0*f_calidad),
calidad_05 = mk_items( 0.8*f_calidad),
calidad_06 = mk_items( 1.2*f_calidad),
calidad_07 = mk_items( 1.0*f_calidad),
calidad_08 = mk_items( 1.1*f_calidad),
calidad_09 = mk_items( 0.9*f_calidad),
calidad_10 = mk_items( 1.0*f_calidad)
)
# 1) Mapa de correlaciones entre ítems (calor) para evidenciar redundancia
corr_df <- encuesta |>
select(-perfil) |>
mutate(across(everything(), as.numeric)) |>
cor() |>
as.data.frame() |>
rownames_to_column("var1") |>
pivot_longer(-var1, names_to = "var2", values_to = "corr")
ggplot(corr_df, aes(var1, var2, fill = corr)) +
geom_tile() +
scale_fill_gradient2(low = "#2166ac", mid = "white", high = "#b2182b", midpoint = 0) +
labs(title = "Mapa de correlaciones entre ítems (30 preguntas)",
subtitle = "Bloques correlacionados sugieren factores latentes (precio, digital, calidad)",
x = NULL, y = NULL, fill = "r") +
theme_minimal(base_size = 11) +
theme(axis.text.x = element_text(angle = 90, vjust = .5, hjust = 1))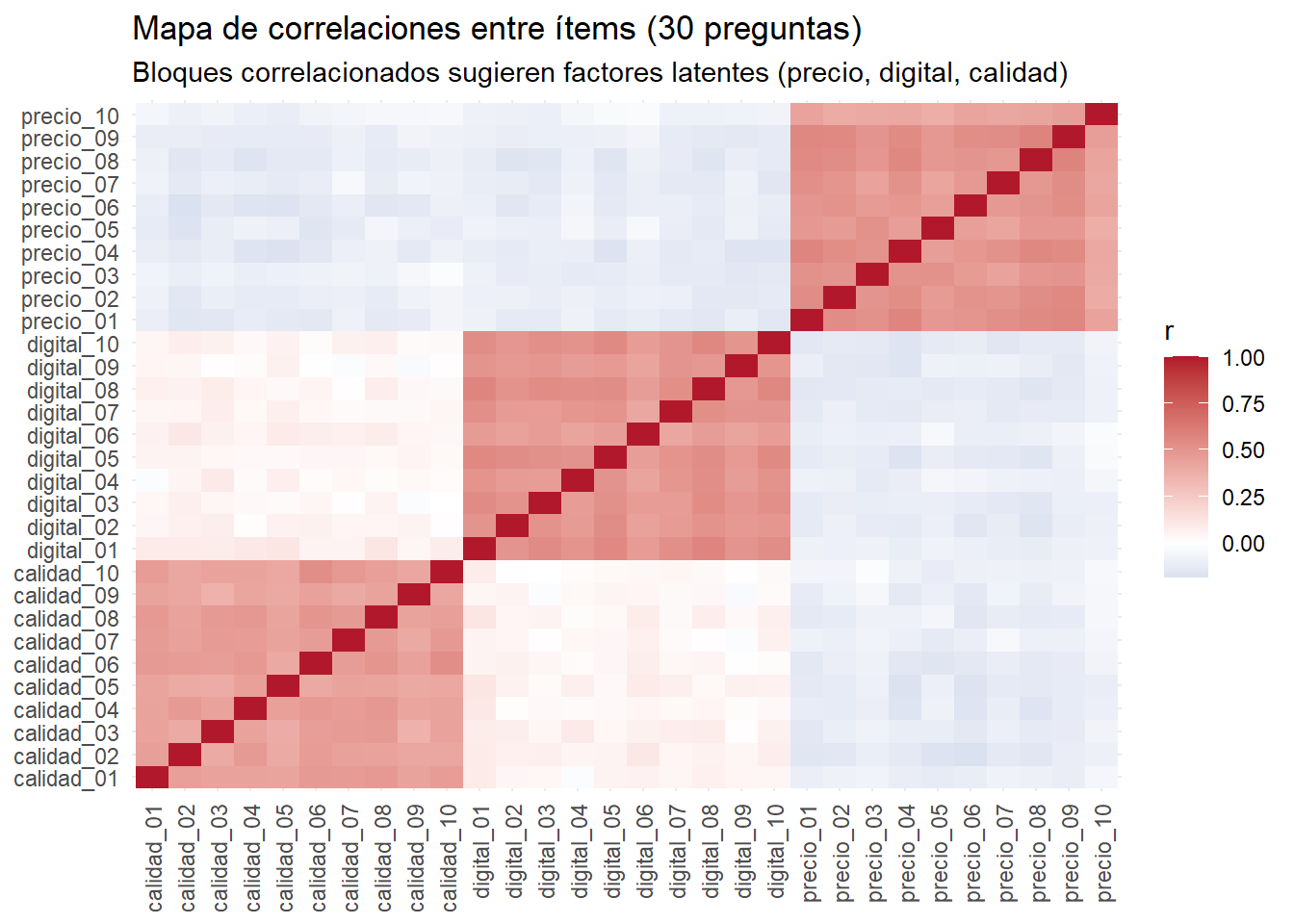
Tienes datos de los mismos países medidos en tres periodos (t = 1, 2 y 3). Para cada país y periodo observas una variable objetivo (por ejemplo, PIB per cápita) y explicativas como inversión y un índice educativo. La meta es explicar cómo cambia Y en función de X respetando que se trata de las mismas unidades repetidas en el tiempo (no muestras distintas cada año).
Pregunta: Antes de ajustar el modelo, ¿qué te dicen los datos sobre la evolución de Y por país y sobre la relación Y–X en cada periodo?
# Panel balanceado: mismos países en t = 1, 2, 3
set.seed(123)
library(tidyverse)
n_paises <- 12
T <- 3
paises <- tibble(pais = factor(paste("País", 1:n_paises)))
panel <- tidyr::expand_grid(pais = paises$pais, t = 1:T) |>
group_by(pais) |>
mutate(
# nivel propio del país (no cambia con el tiempo)
alpha_pais = rnorm(1, 0, 0.7)
) |>
ungroup() |>
# variables explicativas (pueden moverse en el tiempo)
mutate(
inversion = 18 + 2*t + rnorm(n(), 0, 1.5), # % del PIB (crece suave con t)
edu = 9 + 0.3*t + rnorm(n(), 0, 0.4) # índice educativo
) |>
# variable objetivo (PIB pc en escala simulada)
mutate(
y = 8 + 0.25*inversion + 0.7*edu + alpha_pais + rnorm(n(), 0, 0.8)
)
# 1) "Esto es panel": mismas unidades a través del tiempo (slopegraph)
g_panel <- ggplot(panel, aes(x = t, y = y, group = pais, color = pais)) +
geom_line(alpha = 0.5, linewidth = 0.8) +
geom_point(size = 1.8, alpha = 0.8) +
stat_summary(aes(group = 1), fun = mean, geom = "line",
color = "black", linewidth = 1.2, alpha = 0.8) +
stat_summary(aes(group = 1), fun = mean, geom = "point",
color = "black", size = 2.4, alpha = 0.9) +
scale_x_continuous(breaks = 1:3, labels = c("t = 1","t = 2","t = 3")) +
labs(title = "Panel balanceado: mismos países en t = 1, 2 y 3",
subtitle = "Líneas de color: cada país | Línea negra: promedio en cada periodo",
x = NULL, y = "PIB per cápita (escala simulada)", color = "País") +
theme_minimal() +
theme(legend.position = "none")
# 2) Relación Y–X por periodo: Y vs inversión con ajuste lineal, facet por t
g_rel <- ggplot(panel, aes(x = inversion, y = y)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", se = FALSE) +
facet_wrap(~ t, nrow = 1,
labeller = as_labeller(c(`1`="t = 1", `2`="t = 2", `3`="t = 3"))) +
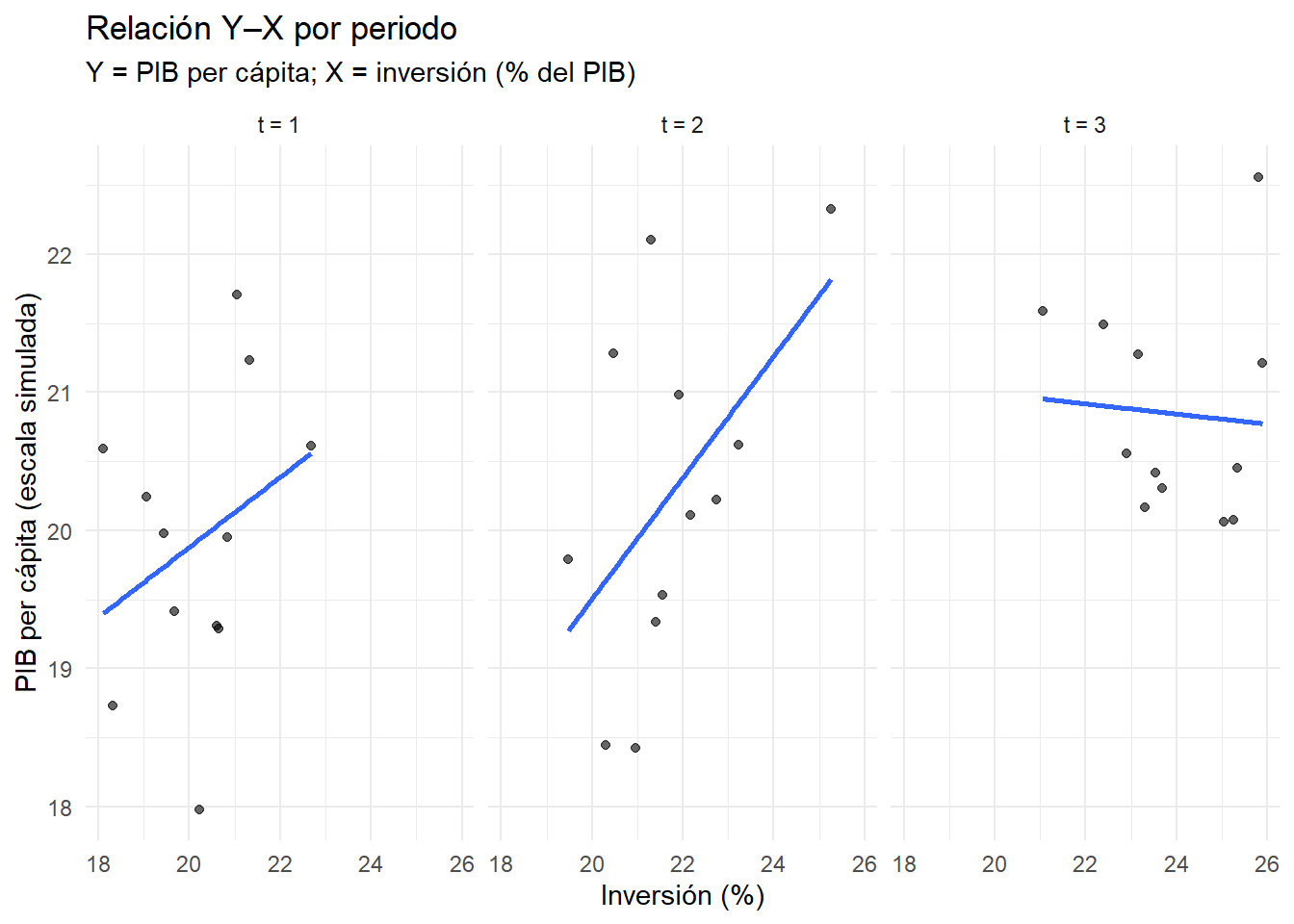
labs(title = "Relación Y–X por periodo",
subtitle = "Y = PIB per cápita; X = inversión (% del PIB)",
x = "Inversión (%)", y = "PIB per cápita (escala simulada)") +
theme_minimal()
g_panel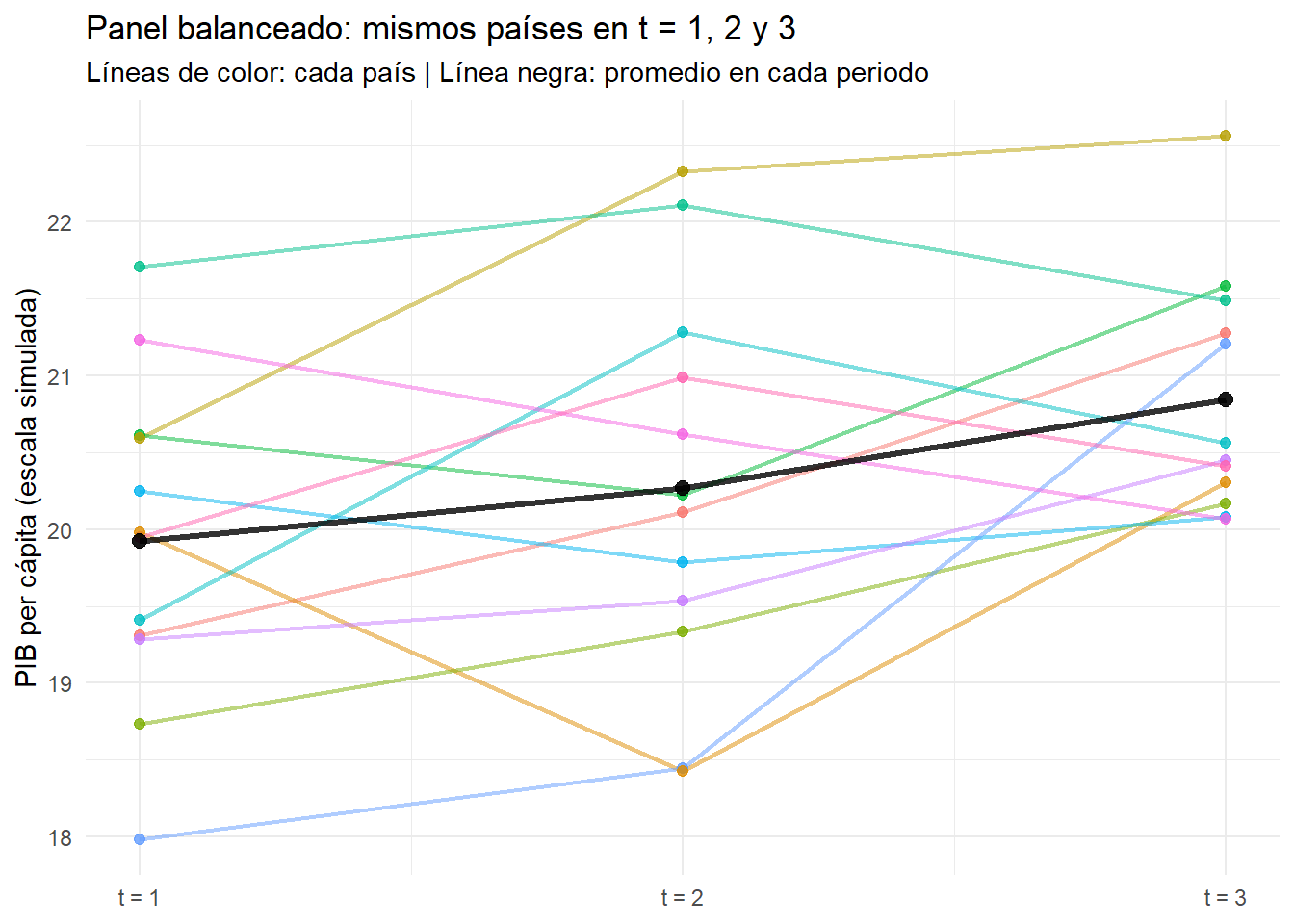
En un país emergente, las autoridades económicas observan que la tasa de interés, el tipo de cambio y el spread de riesgo parecen moverse de forma relacionada. En varias ocasiones, un cambio brusco en una de ellas es seguido, con cierto desfase, por movimientos en las otras. El banco central quiere entender:
Si estos comportamientos están efectivamente conectados.
Cuánto tarda un cambio en una variable en transmitirse a las demás.
Si la dirección de los efectos es siempre la misma o depende del contexto económico.
Pregunta: Con los datos mensuales de estas tres series en los últimos cinco años, ¿cómo identificarías si hay interdependencia y medirías la magnitud y el desfase de los impactos?
set.seed(123)
library(tidyverse)
T <- 60
# Convertimos a numeric para que dplyr::lag no se queje
r_tasa <- as.numeric(arima.sim(list(ar = 0.6), n = T)) * 0.5 + 5
r_tc <- as.numeric(arima.sim(list(ar = 0.5), n = T)) * 20 + 3800 +
dplyr::lag(r_tasa, 1) * 15
r_embi <- as.numeric(arima.sim(list(ar = 0.4), n = T)) * 5 + 200 +
dplyr::lag(r_tc, 1) * 0.05 - dplyr::lag(r_tasa, 1) * 3
df_var <- tibble(
Mes = seq.Date(as.Date("2020-01-01"), by = "month", length.out = T),
`Tasa de interés` = r_tasa,
`Tipo de cambio` = r_tc,
`Spread de riesgo`= r_embi
)
# Visual simple en tres paneles
df_var |>
pivot_longer(-Mes, names_to = "Variable", values_to = "Valor") |>
ggplot(aes(Mes, Valor)) +
geom_line() +
facet_wrap(~ Variable, scales = "free_y", ncol = 1) +
labs(title = "Evolución de tres variables económicas (simulación)",
x = NULL, y = NULL) +
theme_minimal()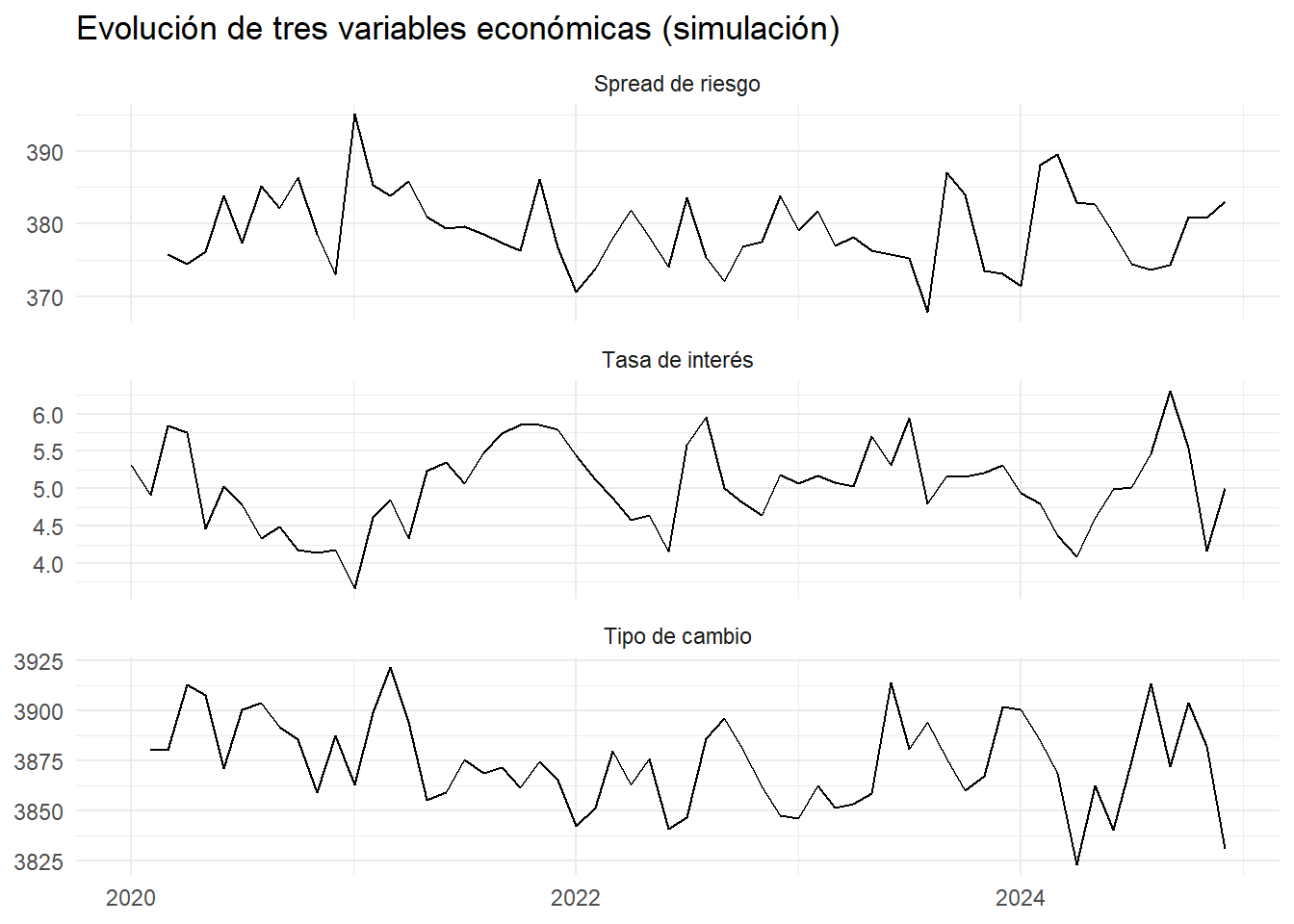
Una empresa de logística registra su demanda diaria durante varios meses. Observa que las ventas parecen aumentar con el tiempo, que hay un patrón que se repite cada semana y que en algunos días festivos o con eventos especiales la demanda cambia bruscamente. El gerente quiere anticipar la demanda futura para optimizar inventarios y personal.
Pregunta: ¿Cómo puedo pronosticar el futuro?
set.seed(11)
library(tidyverse)
library(lubridate)
# 1) Calendario y simulación (≈ 7.5 meses)
inicio <- as.Date("2024-01-01")
T <- 220
fecha <- seq(inicio, by = "day", length.out = T)
t <- seq_along(fecha)
# Patrón: nivel + tendencia + estacionalidad semanal + ruido
nivel <- 500
tend <- 1.3 * t # tendencia creciente
semanal <- 35 * sin(2*pi*t/7) # patrón semanal
ruido <- rnorm(T, 0, 10)
demanda_base <- nivel + tend + semanal + ruido
# 2) Festivos conocidos (dentro del rango) y outliers puntuales
festivos <- as.Date(c("2024-01-01","2024-03-25","2024-03-29","2024-05-01"))
festivos <- festivos[festivos >= min(fecha) & festivos <= max(fecha)]
set.seed(12)
outliers_extra <- sample(fecha[!fecha %in% festivos], 3) # 3 eventos no festivos
# Efectos (ejemplo): algunos suben, otros bajan
efecto_festivo <- ifelse(runif(length(festivos)) > .5, 100, -100)
efecto_outlier <- ifelse(runif(length(outliers_extra)) > .5, 120, -120)
# Aplico efectos
demanda <- demanda_base
demanda[fecha %in% festivos] <- demanda[fecha %in% festivos] + efecto_festivo
demanda[fecha %in% outliers_extra] <- demanda[fecha %in% outliers_extra] + efecto_outlier
# 3) Data frame final
df <- tibble(
Fecha = fecha,
Demanda = demanda,
Semana = wday(fecha, label = TRUE, abbr = TRUE, week_start = 1),
EsFinde = wday(fecha, week_start = 1) %in% c(6,7), # sáb/dom (con week_start = lunes)
Festivo = Fecha %in% festivos,
Outlier = Fecha %in% outliers_extra
)
# 4) Gráfico: serie + tendencia suavizada + marcas de festivos/outliers
ggplot(df, aes(Fecha, Demanda)) +
geom_line(color = "#2C3E50", linewidth = 0.8) +
geom_smooth(se = FALSE, color = "#E74C3C", linetype = "dashed", linewidth = 0.9) +
# marcas de festivos
geom_point(data = subset(df, Festivo), shape = 21, size = 3, stroke = 1,
fill = "#F1C40F", color = "#B7950B") +
# marcas de outliers no festivos
geom_point(data = subset(df, Outlier), shape = 24, size = 3, stroke = 1,
fill = "#5DADE2", color = "#2E86C1") +
# sombrear fines de semana para que se intuya el ciclo semanal
annotate("rect",
xmin = df$Fecha[df$EsFinde & wday(df$Fecha, week_start = 1)==6] - 0.5,
xmax = df$Fecha[df$EsFinde & wday(df$Fecha, week_start = 1)==7] + 0.5,
ymin = -Inf, ymax = Inf, alpha = 0.05, fill = "grey50") +
labs(
title = "Demanda diaria: tendencia, patrón semanal y días especiales (simulación)",
subtitle = "Línea roja: tendencia suavizada | Puntos amarillos: festivos | Triángulos azules: outliers",
x = NULL, y = "Unidades demandadas"
) +
theme_minimal()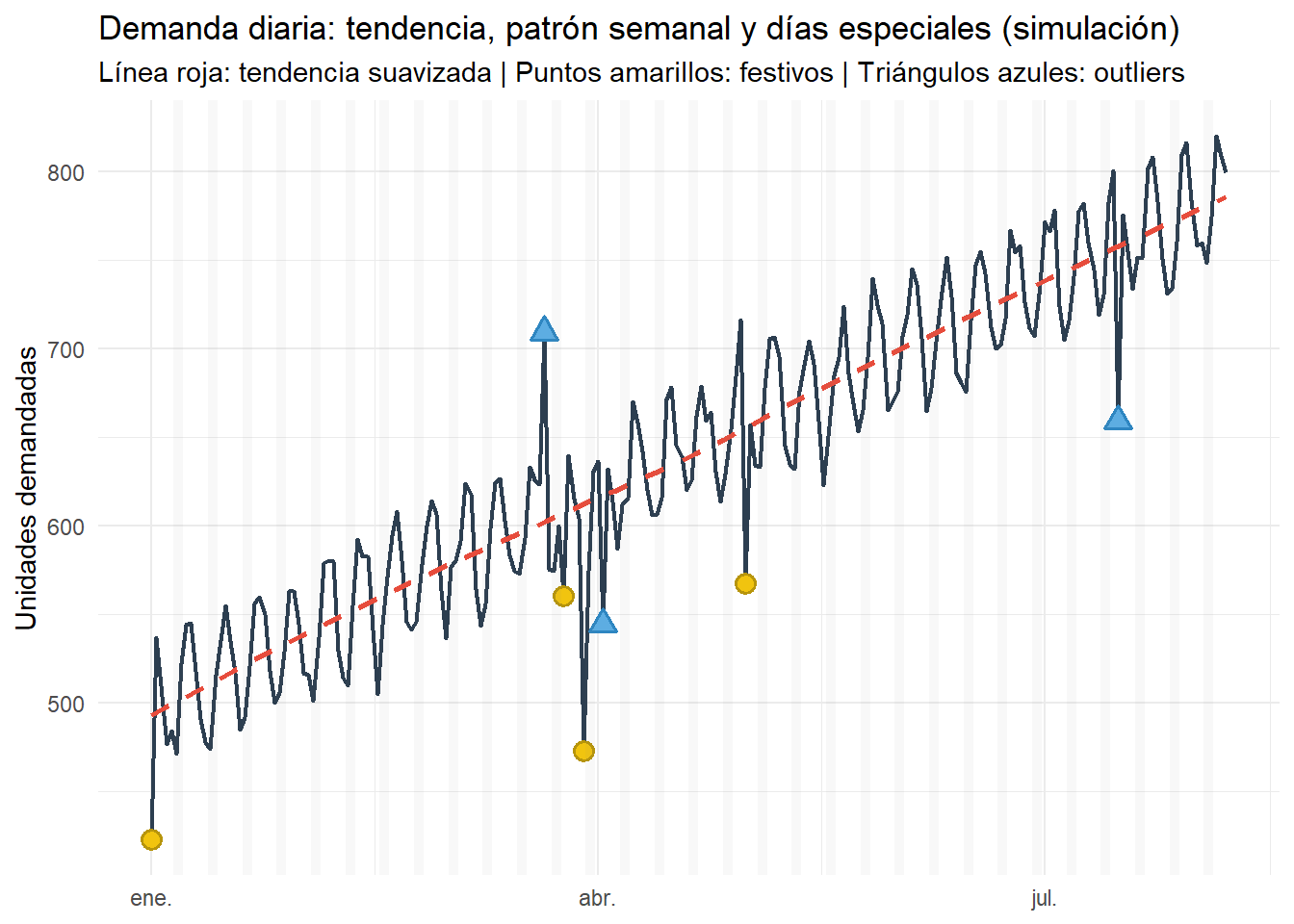
Antes de correr un modelo:
Mapa de flujo (alto nivel):
flowchart TD A[Contexto & Objetivo] --> B[Estructura de Datos] B --> C[EDA & Limpieza] C --> D[Selección de Técnica] D --> E[Modelación: Entrenamiento & Validación] E --> F[Interpretación & Decisión] F --> G[Monitoreo & Mejora]
Patrón frecuente: Empezar por “quiero un VAR/ARIMA/Logit” sin verificar si los datos soportan el supuesto del modelo.
tribble(
~Aspecto, ~R, ~Python,
"Ecosistema estadístico",
"Muy profundo (base + CRAN); econometría madura (AER, plm, vars, quantreg, mgcv, survival, forecast/fable)",
"Amplio, con foco ML/IA (scikit-learn, statsmodels; econometría menos central)",
"Gramática de datos/plot",
"tidyverse/ggplot2: sintaxis declarativa, reproducible",
"pandas/matplotlib: poderoso, a veces más imperativo",
"Reportes reproducibles",
"Quarto/knitr/Rmarkdown nativos",
"Quarto/Jupyter; requiere más pegamento para igualar la experiencia",
"Econometría aplicada",
"Paquetes líderes (plm, lfe/fixest, vars, urca, quantreg, sandwich, clubSandwich)",
"statsmodels cubre parte; panel/VAR menos fluido que en R",
"Curva de aprendizaje",
"R directo a análisis estadístico",
"Python más generalista (software, IA, datos)"
) |>
gt() |>
tab_header(title = "Comparativa práctica R vs Python")| Comparativa práctica R vs Python | ||
|---|---|---|
| Aspecto | R | Python |
| Ecosistema estadístico | Muy profundo (base + CRAN); econometría madura (AER, plm, vars, quantreg, mgcv, survival, forecast/fable) | Amplio, con foco ML/IA (scikit-learn, statsmodels; econometría menos central) |
| Gramática de datos/plot | tidyverse/ggplot2: sintaxis declarativa, reproducible | pandas/matplotlib: poderoso, a veces más imperativo |
| Reportes reproducibles | Quarto/knitr/Rmarkdown nativos | Quarto/Jupyter; requiere más pegamento para igualar la experiencia |
| Econometría aplicada | Paquetes líderes (plm, lfe/fixest, vars, urca, quantreg, sandwich, clubSandwich) | statsmodels cubre parte; panel/VAR menos fluido que en R |
| Curva de aprendizaje | R directo a análisis estadístico | Python más generalista (software, IA, datos) |
Conclusión práctica: Para modelación estadística y econometría aplicada, R ofrece bibliotecas maduras, diagnósticos accesibles y una ruta reproducible (Quarto) con menos fricción.
Recordatorio final: El modelo es un medio, no el fin. Empieza por el porqué y por cómo están tus datos. La técnica correcta es consecuencia de esa reflexión.
R version 4.2.0 (2022-04-22 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 26100)
Matrix products: default
locale:
[1] LC_COLLATE=Spanish_Colombia.utf8 LC_CTYPE=Spanish_Colombia.utf8
[3] LC_MONETARY=Spanish_Colombia.utf8 LC_NUMERIC=C
[5] LC_TIME=Spanish_Colombia.utf8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] gridExtra_2.3 broom_1.0.4 gt_0.5.0 patchwork_1.1.1
[5] lubridate_1.9.2 forcats_1.0.0 stringr_1.5.1 dplyr_1.1.0
[9] purrr_1.0.1 readr_2.1.4 tidyr_1.3.0 tibble_3.2.1
[13] ggplot2_3.5.1 tidyverse_2.0.0
loaded via a namespace (and not attached):
[1] compiler_4.2.0 pillar_1.10.2 tools_4.2.0 digest_0.6.34
[5] checkmate_2.1.0 lattice_0.20-45 nlme_3.1-157 timechange_0.2.0
[9] jsonlite_1.8.8 evaluate_0.23 lifecycle_1.0.4 gtable_0.3.4
[13] mgcv_1.9-1 pkgconfig_2.0.3 rlang_1.1.3 Matrix_1.4-1
[17] cli_3.6.2 rstudioapi_0.15.0 yaml_2.3.8 xfun_0.42
[21] fastmap_1.1.0 withr_3.0.2 knitr_1.45 sass_0.4.8
[25] generics_0.1.3 vctrs_0.6.5 htmlwidgets_1.5.4 hms_1.1.3
[29] grid_4.2.0 tidyselect_1.2.1 glue_1.7.0 R6_2.6.1
[33] rmarkdown_2.25 farver_2.1.1 tzdb_0.3.0 magrittr_2.0.3
[37] splines_4.2.0 backports_1.4.1 scales_1.3.0 htmltools_0.5.7
[41] colorspace_2.1-0 labeling_0.4.3 stringi_1.8.3 munsell_0.5.0 ---
title: "Clase 01 – Introducción"
subtitle: "Contexto de la modelación basada en los datos"
author: "Orlando Joaqui-Barandica"
date: last-modified
format:
html:
toc: true
number-sections: true
code-fold: show
df-print: paged
code-tools: true
theme: cosmo
execute:
echo: true
warning: false
message: false
freeze: auto
editor: visual
---
> **Propósito.** Este documento es la **Clase Introductoria**: una sesión para alinear expectativas, pensar en *problemas reales* y mapearlos a técnicas. No es un set de diapositivas; es un material reproducible: texto + código + figuras.
::: callout-tip
## Cómo usar este documento
- Lee cada contexto y piensa primero en **la pregunta** y **la estructura de los datos**, *antes* de proponer un modelo.
- Ejecuta los chunks de R para explorar visualmente y anota *supuestos* y *riesgos*.
- Vuelve a este documento durante el curso como mapa general de decisiones.
:::
## Setup del entorno
```{r}
#| label: setup
#| include: true
# Paquetes sugeridos para la clase
# install.packages(c("tidyverse","patchwork","gt","pROC","broom","modelsummary"))
library(tidyverse)
library(patchwork)
library(gt)
library(broom)
```
## Contextos
> Objetivo: iniciar con preguntas casuales pero profundas. Por cada contexto, **¿qué mirarías antes de elegir la técnica?**
### Ventas y precio
::: {.callout-note appearance="simple"}
## Contexto
Una cadena minorista ha notado variaciones importantes en las ventas de uno de sus productos y sospecha que el precio, las promociones y la estacionalidad están influyendo. Para tomar decisiones informadas, necesita analizar datos de 24 meses que incluyen ventas, precio promedio y gasto en promoción, con el fin de identificar patrones y estimar cómo cambios en el precio podrían impactar la demanda.
Entonces:
Imagina que trabajas para una cadena de tiendas y te piden encontrar el "punto justo" de precio para uno de sus productos estrella. Tienes sobre la mesa dos años de datos: cuánto se vendió cada mes, el precio promedio, el gasto en promociones y si fue temporada alta o baja. La gerencia quiere entender cómo ajustar el precio para vender más sin perder rentabilidad, y tu misión es descubrirlo usando los datos.
:::
**Pregunta:** ¿Cuál es el problema?, ¿Cuál es la estructura de datos a la cuál te estás enfrentando?, etc. etc. etc.
```{r}
# Simulación mínima para ambientar
df_vtas <- tibble(
mes = 1:24,
promo = rbinom(24, 1, .4),
precio = round(rnorm(24, mean = 10, sd = 1.2), 2),
estac = rep(c("alta","baja"), each = 12)
) |>
mutate(ventas = round( 2000 * precio^(-1.3) * ifelse(promo==1, 1.15, 1) * ifelse(estac=="alta", 1.2, 0.9)
* exp(rnorm(24, 0, .1)) ))
g1 <- ggplot(df_vtas, aes(precio, ventas, shape = estac, color = factor(promo))) +
geom_point(size = 3, alpha = .8) +
scale_color_manual(
values = c("0" = "gray50", "1" = "tomato"),
labels = c("Sin promoción", "Con promoción"),
name = "Promoción"
) +
labs(
title = "Relación Precio–Ventas (simulación)",
x = "Precio",
y = "Ventas"
) +
theme_minimal()
g1
```
------------------------------------------------------------------------
### Desigualdad de efectos
::: {.callout-note appearance="simple"}
## Contexto
En un plan de incentivos, la gerencia quiere saber si el bono ayuda más a quienes menos ganan o si el efecto es similar para todos. La pregunta ya no es "¿cuánto sube el salario promedio?", sino "¿qué pasa en los extremos?": ¿mejora especialmente la situación de los de abajo?, ¿casi no cambia en los de arriba?, ¿se mueve toda la distribución por igual?
:::
**Pregunta:** Si lo que importa es cómo cambian las colas (los salarios más bajos y más altos), ¿tiene sentido seguir mirando solo el promedio? ¿Qué métricas o gráficos usarías para comparar abajo, centro y arriba de la distribución?
```{r}
# Ambientación: relación simulada con heterocedasticidad
# Simulación: el bono favorece más a quienes menos ganan
set.seed(123)
library(dplyr)
library(tidyr)
library(ggplot2)
n <- 1000
base <- rlnorm(n, meanlog = 11, sdlog = 0.45) # salarios base (sesgados a la derecha)
# El bono impacta más fuerte en la parte baja, medio en el centro y leve en la alta
q30 <- quantile(base, 0.30)
q70 <- quantile(base, 0.70)
efecto <- ifelse(base <= q30, 0.12,
ifelse(base <= q70, 0.05, 0.01))
despues <- base * (1 + efecto)
datos <- tibble(
salario = c(base, despues),
estado = rep(c("Antes del bono", "Después del bono"), each = n)
)
# Cálculo de cuantiles para marcar (10%, 50%, 90%) en cada estado
df_q <- datos %>%
group_by(estado) %>%
summarize(
q10 = quantile(salario, 0.10),
q50 = quantile(salario, 0.50),
q90 = quantile(salario, 0.90),
.groups = "drop"
) %>%
pivot_longer(cols = starts_with("q"), names_to = "quantil", values_to = "valor")
# Histograma superpuesto con líneas en 10-50-90
g2<- ggplot(datos, aes(salario, fill = estado)) +
geom_histogram(position = "identity", alpha = 0.35, bins = 40) +
geom_vline(data = df_q, aes(xintercept = valor, color = estado, linetype = quantil),
linewidth = 0.6, show.legend = TRUE) +
scale_fill_manual(values = c("Antes del bono" = "gray50", "Después del bono" = "steelblue")) +
scale_color_manual(values = c("Antes del bono" = "gray50", "Después del bono" = "steelblue")) +
labs(
title = "Distribución salarial antes y después del bono",
subtitle = "Líneas verticales: 10º, 50º (mediana) y 90º percentil por estado",
x = "Salario", y = "Frecuencia", fill = "Estado", color = "Estado", linetype = "Cuantil"
) +
theme_minimal()
g2
```
- ¿El bono "empuja" más la parte baja que la alta?
- Si solo miraras el promedio, ¿te perderías este matiz?
- ¿Qué otras comparaciones harías entre abajo--centro--arriba para decidir si la política cumple su objetivo?
------------------------------------------------------------------------
### Decidir entre alternativas
::: {.callout-note appearance="simple"}
## Contexto
Un banco lanza un nuevo producto digital y ve baja adopción. No puede ofrecerlo indiscriminadamente: cada contacto cuesta, y hay tres planes (básico/estándar/premium) con estructuras de comisión distintas. El equipo quiere entender quiénes tienden a adoptar (sí/no) y, entre quienes adoptan, qué plan eligen. Sospechan que ingreso y edad influyen, pero también hay estacionalidad de campañas y límites de presupuesto. Antes de hablar de métricas avanzadas, la primera pregunta práctica es: ¿las distribuciones de ingreso/edad se ven distintas entre quienes adoptan y quienes no? Y, entre los que sí, ¿se diferencian según el plan?
:::
**Pregunta:** Si las distribuciones por grupo son claramente distintas, ¿no sugiere eso probabilidades de adopción diferentes? ¿Cómo lo mostrarías de forma simple y convincente antes de construir el modelo?
```{r}
# Simulación y boxplots (adopción y elección de plan) — versión robusta
set.seed(1)
library(tidyverse)
library(gridExtra)
n <- 1200
pros <- tibble(
ingreso = rlnorm(n, meanlog = 10.2, sdlog = 0.45),
edad = pmax(18, rnorm(n, mean = 36, sd = 9))
) |>
# prob. de adopción: crece con ingreso y edad
mutate(lp = -8 + 0.00006*ingreso + 0.028*edad,
p_adopta = 1/(1 + exp(-lp)),
adopta = rbinom(n, 1, p_adopta)) |>
# utilidades para planes SOLO si adopta (balanceadas + ruido)
rowwise() |>
mutate(
u_basico = 0.10 + 0.000015*ingreso + 0.004*edad + rnorm(1, 0, 0.15),
u_estandar = 0.00 + 0.000020*ingreso + 0.003*edad + rnorm(1, 0, 0.15),
u_premium = -0.10 + 0.000035*ingreso + 0.001*edad + rnorm(1, 0, 0.15),
plan = if (adopta == 1) {
exps <- exp(c(u_basico, u_estandar, u_premium))
c("Básico","Estándar","Premium")[sample(1:3, 1, prob = exps/sum(exps))]
} else NA_character_
) |>
ungroup() |>
mutate(
grupo = factor(adopta, levels = c(0,1), labels = c("No adopta","Adopta")),
plan = factor(plan, levels = c("Básico","Estándar","Premium"))
)
# Boxplots: ¿ingreso/edad difieren entre No adopta vs Adopta?
p_ing <- ggplot(pros, aes(grupo, ingreso)) +
geom_boxplot(outlier.alpha = 0.25) +
scale_y_continuous(labels = scales::label_number(scale_cut = scales::cut_si(" "))) +
labs(title = "Ingreso por grupo de adopción", x = NULL, y = "Ingreso") +
theme_minimal()
p_edad <- ggplot(pros, aes(grupo, edad)) +
geom_boxplot(outlier.alpha = 0.25) +
labs(title = "Edad por grupo de adopción", x = NULL, y = "Edad") +
theme_minimal()
# Entre los que adoptan: ingreso por plan (forzamos el orden de niveles)
p_plan <- pros |>
filter(adopta == 1) |>
ggplot(aes(plan, ingreso)) +
geom_boxplot(outlier.alpha = 0.25) +
scale_x_discrete(drop = FALSE) + # respeta los 3 niveles
scale_y_continuous(labels = scales::label_number(scale_cut = scales::cut_si(" "))) +
labs(title = "Ingreso entre adoptantes, por plan", x = NULL, y = "Ingreso") +
theme_minimal()
gridExtra::grid.arrange(
p_ing, p_edad, p_plan,
layout_matrix = rbind(c(1,2),
c(3,3))
)
```
------------------------------------------------------------------------
### Caracterizar la población
::: {.callout-note appearance="simple"}
## Contexto
Aplicaste una encuesta con 30 preguntas tipo Likert (1--5) sobre hábitos de compra, sensibilidad al precio, uso de canales digitales y percepción de calidad/servicio. El equipo quiere crear segmentos útiles para marketing y diseño de producto (por ejemplo, "ahorradores", "buscan conveniencia", "premium"), pero con tantas preguntas hay redundancia y ruido: varias ítems parecen medir lo mismo y es difícil explicar los resultados a gerencia.
:::
**Pregunta:** ¿Tiene sentido comprimir las 30 preguntas en pocas dimensiones interpretables (p.ej., "sensibilidad al precio", "afinidad digital", "búsqueda de calidad") y luego segmentar? ¿Cómo decidir cuántas dimensiones y cuántos segmentos mantener sin perder interpretabilidad?
```{r}
# Simulación realista: 30 ítems Likert con 3 factores latentes
set.seed(7)
library(tidyverse)
n <- 800
# tres perfiles latentes (solo para simular): Ahorrador / Conveniencia / Premium
perfil <- sample(c("Ahorrador","Conveniencia","Premium"), n, replace = TRUE, prob = c(.4,.35,.25))
# factores latentes por persona (no observables)
f_precio <- rnorm(n, ifelse(perfil=="Ahorrador", 0.8, ifelse(perfil=="Conveniencia", 0.1, -0.4)), 0.6)
f_digital <- rnorm(n, ifelse(perfil=="Conveniencia",0.7, ifelse(perfil=="Premium", 0.3, -0.2)), 0.6)
f_calidad <- rnorm(n, ifelse(perfil=="Premium", 0.8, ifelse(perfil=="Conveniencia", 0.2, 0.1)), 0.6)
# 30 items (10 por factor) + ruido; mapeo a escala 1-5
mk_items <- function(base, s = .6) pmin(5, pmax(1, round(scales::rescale(base + rnorm(n,0,s), to = c(1,5)))))
encuesta <- tibble(
perfil,
# 10 ítems que cargan en "precio"
precio_01 = mk_items( 1.2*f_precio),
precio_02 = mk_items( 1.0*f_precio),
precio_03 = mk_items( 0.9*f_precio),
precio_04 = mk_items( 1.1*f_precio),
precio_05 = mk_items( 0.8*f_precio),
precio_06 = mk_items( 1.0*f_precio),
precio_07 = mk_items( 1.0*f_precio),
precio_08 = mk_items( 0.9*f_precio),
precio_09 = mk_items( 1.1*f_precio),
precio_10 = mk_items( 0.7*f_precio),
# 10 ítems que cargan en "digital"
digital_01 = mk_items( 1.1*f_digital),
digital_02 = mk_items( 1.0*f_digital),
digital_03 = mk_items( 0.9*f_digital),
digital_04 = mk_items( 1.0*f_digital),
digital_05 = mk_items( 1.1*f_digital),
digital_06 = mk_items( 0.8*f_digital),
digital_07 = mk_items( 1.0*f_digital),
digital_08 = mk_items( 1.2*f_digital),
digital_09 = mk_items( 0.9*f_digital),
digital_10 = mk_items( 1.0*f_digital),
# 10 ítems que cargan en "calidad"
calidad_01 = mk_items( 1.1*f_calidad),
calidad_02 = mk_items( 1.0*f_calidad),
calidad_03 = mk_items( 0.9*f_calidad),
calidad_04 = mk_items( 1.0*f_calidad),
calidad_05 = mk_items( 0.8*f_calidad),
calidad_06 = mk_items( 1.2*f_calidad),
calidad_07 = mk_items( 1.0*f_calidad),
calidad_08 = mk_items( 1.1*f_calidad),
calidad_09 = mk_items( 0.9*f_calidad),
calidad_10 = mk_items( 1.0*f_calidad)
)
# 1) Mapa de correlaciones entre ítems (calor) para evidenciar redundancia
corr_df <- encuesta |>
select(-perfil) |>
mutate(across(everything(), as.numeric)) |>
cor() |>
as.data.frame() |>
rownames_to_column("var1") |>
pivot_longer(-var1, names_to = "var2", values_to = "corr")
ggplot(corr_df, aes(var1, var2, fill = corr)) +
geom_tile() +
scale_fill_gradient2(low = "#2166ac", mid = "white", high = "#b2182b", midpoint = 0) +
labs(title = "Mapa de correlaciones entre ítems (30 preguntas)",
subtitle = "Bloques correlacionados sugieren factores latentes (precio, digital, calidad)",
x = NULL, y = NULL, fill = "r") +
theme_minimal(base_size = 11) +
theme(axis.text.x = element_text(angle = 90, vjust = .5, hjust = 1))
```
------------------------------------------------------------------------
### Comparaciones longitudinales
::: {.callout-note appearance="simple"}
## Contexto
Tienes datos de los mismos países medidos en tres periodos (t = 1, 2 y 3). Para cada país y periodo observas una variable objetivo (por ejemplo, PIB per cápita) y explicativas como inversión y un índice educativo. La meta es explicar cómo cambia Y en función de X respetando que se trata de las mismas unidades repetidas en el tiempo (no muestras distintas cada año).
:::
**Pregunta:** Antes de ajustar el modelo, ¿qué te dicen los datos sobre la evolución de Y por país y sobre la relación Y--X en cada periodo?
```{r}
# Panel balanceado: mismos países en t = 1, 2, 3
set.seed(123)
library(tidyverse)
n_paises <- 12
T <- 3
paises <- tibble(pais = factor(paste("País", 1:n_paises)))
panel <- tidyr::expand_grid(pais = paises$pais, t = 1:T) |>
group_by(pais) |>
mutate(
# nivel propio del país (no cambia con el tiempo)
alpha_pais = rnorm(1, 0, 0.7)
) |>
ungroup() |>
# variables explicativas (pueden moverse en el tiempo)
mutate(
inversion = 18 + 2*t + rnorm(n(), 0, 1.5), # % del PIB (crece suave con t)
edu = 9 + 0.3*t + rnorm(n(), 0, 0.4) # índice educativo
) |>
# variable objetivo (PIB pc en escala simulada)
mutate(
y = 8 + 0.25*inversion + 0.7*edu + alpha_pais + rnorm(n(), 0, 0.8)
)
# 1) "Esto es panel": mismas unidades a través del tiempo (slopegraph)
g_panel <- ggplot(panel, aes(x = t, y = y, group = pais, color = pais)) +
geom_line(alpha = 0.5, linewidth = 0.8) +
geom_point(size = 1.8, alpha = 0.8) +
stat_summary(aes(group = 1), fun = mean, geom = "line",
color = "black", linewidth = 1.2, alpha = 0.8) +
stat_summary(aes(group = 1), fun = mean, geom = "point",
color = "black", size = 2.4, alpha = 0.9) +
scale_x_continuous(breaks = 1:3, labels = c("t = 1","t = 2","t = 3")) +
labs(title = "Panel balanceado: mismos países en t = 1, 2 y 3",
subtitle = "Líneas de color: cada país | Línea negra: promedio en cada periodo",
x = NULL, y = "PIB per cápita (escala simulada)", color = "País") +
theme_minimal() +
theme(legend.position = "none")
# 2) Relación Y–X por periodo: Y vs inversión con ajuste lineal, facet por t
g_rel <- ggplot(panel, aes(x = inversion, y = y)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", se = FALSE) +
facet_wrap(~ t, nrow = 1,
labeller = as_labeller(c(`1`="t = 1", `2`="t = 2", `3`="t = 3"))) +
labs(title = "Relación Y–X por periodo",
subtitle = "Y = PIB per cápita; X = inversión (% del PIB)",
x = "Inversión (%)", y = "PIB per cápita (escala simulada)") +
theme_minimal()
g_panel
g_rel
```
------------------------------------------------------------------------
### Interacciones dinámicas
::: {.callout-note appearance="simple"}
## Contexto
En un país emergente, las autoridades económicas observan que la tasa de interés, el tipo de cambio y el spread de riesgo parecen moverse de forma relacionada. En varias ocasiones, un cambio brusco en una de ellas es seguido, con cierto desfase, por movimientos en las otras. El banco central quiere entender:
Si estos comportamientos están efectivamente conectados.
Cuánto tarda un cambio en una variable en transmitirse a las demás.
Si la dirección de los efectos es siempre la misma o depende del contexto económico.
:::
**Pregunta:** Con los datos mensuales de estas tres series en los últimos cinco años, ¿cómo identificarías si hay interdependencia y medirías la magnitud y el desfase de los impactos?
```{r}
set.seed(123)
library(tidyverse)
T <- 60
# Convertimos a numeric para que dplyr::lag no se queje
r_tasa <- as.numeric(arima.sim(list(ar = 0.6), n = T)) * 0.5 + 5
r_tc <- as.numeric(arima.sim(list(ar = 0.5), n = T)) * 20 + 3800 +
dplyr::lag(r_tasa, 1) * 15
r_embi <- as.numeric(arima.sim(list(ar = 0.4), n = T)) * 5 + 200 +
dplyr::lag(r_tc, 1) * 0.05 - dplyr::lag(r_tasa, 1) * 3
df_var <- tibble(
Mes = seq.Date(as.Date("2020-01-01"), by = "month", length.out = T),
`Tasa de interés` = r_tasa,
`Tipo de cambio` = r_tc,
`Spread de riesgo`= r_embi
)
# Visual simple en tres paneles
df_var |>
pivot_longer(-Mes, names_to = "Variable", values_to = "Valor") |>
ggplot(aes(Mes, Valor)) +
geom_line() +
facet_wrap(~ Variable, scales = "free_y", ncol = 1) +
labs(title = "Evolución de tres variables económicas (simulación)",
x = NULL, y = NULL) +
theme_minimal()
```
------------------------------------------------------------------------
### Pronóstico
::: {.callout-note appearance="simple"}
## Contexto
Una empresa de logística registra su demanda diaria durante varios meses. Observa que las ventas parecen aumentar con el tiempo, que hay un patrón que se repite cada semana y que en algunos días festivos o con eventos especiales la demanda cambia bruscamente. El gerente quiere anticipar la demanda futura para optimizar inventarios y personal.
:::
**Pregunta:** ¿Cómo puedo pronosticar el *futuro*?
```{r}
#| label: grafico-pronostico
#| echo: true
set.seed(11)
library(tidyverse)
library(lubridate)
# 1) Calendario y simulación (≈ 7.5 meses)
inicio <- as.Date("2024-01-01")
T <- 220
fecha <- seq(inicio, by = "day", length.out = T)
t <- seq_along(fecha)
# Patrón: nivel + tendencia + estacionalidad semanal + ruido
nivel <- 500
tend <- 1.3 * t # tendencia creciente
semanal <- 35 * sin(2*pi*t/7) # patrón semanal
ruido <- rnorm(T, 0, 10)
demanda_base <- nivel + tend + semanal + ruido
# 2) Festivos conocidos (dentro del rango) y outliers puntuales
festivos <- as.Date(c("2024-01-01","2024-03-25","2024-03-29","2024-05-01"))
festivos <- festivos[festivos >= min(fecha) & festivos <= max(fecha)]
set.seed(12)
outliers_extra <- sample(fecha[!fecha %in% festivos], 3) # 3 eventos no festivos
# Efectos (ejemplo): algunos suben, otros bajan
efecto_festivo <- ifelse(runif(length(festivos)) > .5, 100, -100)
efecto_outlier <- ifelse(runif(length(outliers_extra)) > .5, 120, -120)
# Aplico efectos
demanda <- demanda_base
demanda[fecha %in% festivos] <- demanda[fecha %in% festivos] + efecto_festivo
demanda[fecha %in% outliers_extra] <- demanda[fecha %in% outliers_extra] + efecto_outlier
# 3) Data frame final
df <- tibble(
Fecha = fecha,
Demanda = demanda,
Semana = wday(fecha, label = TRUE, abbr = TRUE, week_start = 1),
EsFinde = wday(fecha, week_start = 1) %in% c(6,7), # sáb/dom (con week_start = lunes)
Festivo = Fecha %in% festivos,
Outlier = Fecha %in% outliers_extra
)
# 4) Gráfico: serie + tendencia suavizada + marcas de festivos/outliers
ggplot(df, aes(Fecha, Demanda)) +
geom_line(color = "#2C3E50", linewidth = 0.8) +
geom_smooth(se = FALSE, color = "#E74C3C", linetype = "dashed", linewidth = 0.9) +
# marcas de festivos
geom_point(data = subset(df, Festivo), shape = 21, size = 3, stroke = 1,
fill = "#F1C40F", color = "#B7950B") +
# marcas de outliers no festivos
geom_point(data = subset(df, Outlier), shape = 24, size = 3, stroke = 1,
fill = "#5DADE2", color = "#2E86C1") +
# sombrear fines de semana para que se intuya el ciclo semanal
annotate("rect",
xmin = df$Fecha[df$EsFinde & wday(df$Fecha, week_start = 1)==6] - 0.5,
xmax = df$Fecha[df$EsFinde & wday(df$Fecha, week_start = 1)==7] + 0.5,
ymin = -Inf, ymax = Inf, alpha = 0.05, fill = "grey50") +
labs(
title = "Demanda diaria: tendencia, patrón semanal y días especiales (simulación)",
subtitle = "Línea roja: tendencia suavizada | Puntos amarillos: festivos | Triángulos azules: outliers",
x = NULL, y = "Unidades demandadas"
) +
theme_minimal()
```
## Filosofía del curso: del contexto a la técnica
Antes de correr un modelo:
- **Problema**: propósito de negocio/política → métrica de decisión.
- **Contexto**: supuestos razonables (comportamiento, restricciones, costos).
- **Datos**: unidad de análisis, granularidad, periodo, sesgos, faltantes.
- **Medición**: calidad de variables (proxy, escalas, transformaciones).
- **Validación**: supuestos del modelo, backtesting, sensibilidad.
- **Comunicación**: narrativa, incertidumbre, límites.
**Mapa de flujo (alto nivel)**:
```{mermaid}
flowchart TD
A[Contexto & Objetivo] --> B[Estructura de Datos]
B --> C[EDA & Limpieza]
C --> D[Selección de Técnica]
D --> E[Modelación: Entrenamiento & Validación]
E --> F[Interpretación & Decisión]
F --> G[Monitoreo & Mejora]
```
::: callout-warning
**Patrón frecuente:** Empezar por "quiero un VAR/ARIMA/Logit" sin verificar si los **datos** soportan el supuesto del modelo.
:::
## **R** vs **Python** (y por qué R brilla en modelación estadística)
```{r}
tribble(
~Aspecto, ~R, ~Python,
"Ecosistema estadístico",
"Muy profundo (base + CRAN); econometría madura (AER, plm, vars, quantreg, mgcv, survival, forecast/fable)",
"Amplio, con foco ML/IA (scikit-learn, statsmodels; econometría menos central)",
"Gramática de datos/plot",
"tidyverse/ggplot2: sintaxis declarativa, reproducible",
"pandas/matplotlib: poderoso, a veces más imperativo",
"Reportes reproducibles",
"Quarto/knitr/Rmarkdown nativos",
"Quarto/Jupyter; requiere más pegamento para igualar la experiencia",
"Econometría aplicada",
"Paquetes líderes (plm, lfe/fixest, vars, urca, quantreg, sandwich, clubSandwich)",
"statsmodels cubre parte; panel/VAR menos fluido que en R",
"Curva de aprendizaje",
"R directo a análisis estadístico",
"Python más generalista (software, IA, datos)"
) |>
gt() |>
tab_header(title = "Comparativa práctica R vs Python")
```
::: callout-tip
**Conclusión práctica:** Para **modelación estadística y econometría aplicada**, R ofrece **bibliotecas maduras**, **diagnósticos accesibles** y una **ruta reproducible** (Quarto) con menos fricción.
:::
## Las **7 temáticas** del curso (qué, cuándo, cómo)
### Regresión lineal múltiple
- **Qué resuelve:** relaciones promedio y **elasticidades**.
- **Datos típicos:** cross-section o panel corto; transformaciones log.
- **Claves:** multicolinealidad, escalas, outliers, supuestos de Gauss--Markov.
- **Métricas:** R² ajustado, RMSE, AIC; IC de elasticidades.
- **Errores comunes:** interpretar causalidad sin diseño; no revisar residuos.
### Modelo cuantilíco
- **Qué resuelve:** **heterogeneidad** de efectos a lo largo de la distribución.
- **Claves:** elección de **taus**; bandas de confianza; robustez a outliers.
- **Comunicación:** fan plots de coeficientes por tau.
### Modelos de elección discreta
- **Qué resuelve:** decisiones **sí/no** o **multicategoría**.
- **Claves:** escalas de variables, separación completa, desbalance.
- **Métricas:** ROC/, sensibilidad/especificidad.
### Reducción de dimensionalidad y segmentación
- **Qué resuelve:** **separar señal de ruido** y crear **perfiles**.
- **Claves:** estandarización, número de componentes, estabilidad de clusters.
- **Validación:** proporción de varianza, silhouette, sensibilidad a inicialización.
### Modelos de datos de panel
- **Qué resuelve:** heterogeneidad **no observada** y comparaciones en el tiempo.
- **Claves:** FE vs RE, Hausman, errores estándar robustos (clusterizados).
### Modelos VAR
- **Qué resuelve:** **dinámica conjunta**, causalidad de Granger, choques.
- **Claves:** estacionariedad, rezagos, identificación, IRFs con intervalos.
### Series de tiempo
- **Qué resuelve:** tendencia/estacionalidad/shocks, pronósticos con **ARIMA**.
- **Claves:** diferenciación, estacionalidad múltiple, calendario (festivos).
## **Problemas para discusión**
### Caso A -- Pricing con restricciones de canal
- **Situación:** optimizar precios en 50 productos con **restricciones de margen** y **canibalización** entre productos.
- **Retos:** colinealidad entre precio y promo; estacionalidad; variables instrumentales.
- **Posible enfoque:** modelos log-log por categoría + efectos fijos de producto; o **modelo jerárquico**.
### Caso B -- Efectos heterogéneos en política salarial
- **Situación:** un bono impacta distinto en percentiles bajos/altos.
- **Retos:** selección; medición de productividad; **cuantilíco** con covariables.
- **Posible enfoque:** regresión cuantilíca por **taus = 0.1...0.9** con bandas.
### Caso C -- Adopción con clases desbalanceadas
- **Situación:** adopta = 1 en 8% de los casos.
- **Retos:** **desbalance**; separación; costo asimétrico de errores.
- **Posible enfoque:** **logit** con *class weights*, umbral óptimo por **curva coste--beneficio**; validación temporal.
### Caso D -- Segmentación interpretable con 40 variables
- **Situación:** encuesta con 40 ítems; directivos piden **segmentos accionables**.
- **Retos:** interpretabilidad de componentes; **clúster inestable**.
- **Posible enfoque:** **ACP** + **k-medias**; estabilidad vía *bootstrap*; perfiles con gráficos de radar.
### Caso E -- Panel con tratamiento escalonado
- **Situación:** la política se implementa en años diferentes por empresa.
- **Retos:** **heterogeneidad dinámica**; correlación serial.
- **Posible enfoque:** FE con errores clusterizados por empresa + leads/lags del tratamientos.
### Caso F -- VAR con cambios de régimen
- **Situación:** relaciones macro cambian post-choque externo.
- **Retos:** **no estacionariedad** estructural; ventanas móviles.
- **Posible enfoque:** VAR por submuestras; IRFs comparadas.
### Caso G -- Pronóstico con festivos y outliers
- **Situación:** demanda diaria con picos en promociones y festivos.
- **Retos:** múltiples estacionalidades; eventos exógenos.
- **Posible enfoque:** ARIMA con dummies de calendario; comparar con modelos aditivos (GAM/Prophet como benchmark).
## Expectativas y evaluación (resumen)
- **Contexto primero:** cada taller inicia con **planteamiento del problema**.
- **Datos limpios:** documenta supuestos, faltantes y transformaciones.
- **Modelo transparente:** justifica la técnica.
- **Interpretación y decisión:** conecta con la métrica de negocio.
::: callout-tip
**Recordatorio final:** *El modelo es un medio, no el fin.* Empieza por el **porqué** y por **cómo están tus datos**. La técnica correcta es consecuencia de esa reflexión.
:::
```{r}
sessionInfo()
```